Friday's Test Topics
Here’s a list of topics for Friday’s test:
Precalculus Chapter 5 Test Topics:
Composite Argument Properties (memorize! – sine and cosine)
Double Argument Properties (sine and cosine)
Understanding the implications of the +/- in the half-argument properties
Composition of Ordinates – sketch the graph of the sum or product of two given functions
Discussion/Illustration of co-function and odd/even properties
Numeric proof/demonstration of Composite Argument properties
Transform an equation given in terms of cosine with a phase displacement to a linear combination of sine and cosine
Transform an equation given as a linear combination of sine and cosine to an equation in terms of cosine with a phase displacement
Use a composite argument property to prove a co-function property
Use given values to compute composite functions
Compare algebraic computed values to calculator values
Harmonic analysis
Terminology
Composite Argument Identity
Application of Sum and Product Properties
Application of ½ -angle Properties
That’s it! The format is as expected – ½ calculator, ½ non-calculator. The calculator portion is significantly longer than the non-calculator portion, so budget your time accordingly. I’ll be in my classroom on Thursday after school and before school on Friday. I’ll also be available online later on Thursday evening. If you have specific questions Thursday night, email me!
See you in class!
"The best way to predict your future is to create it."
- Peter Drucker


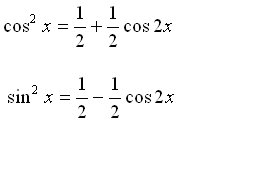

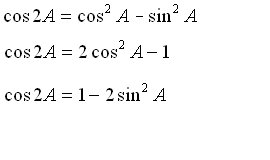
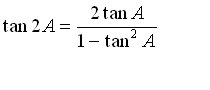


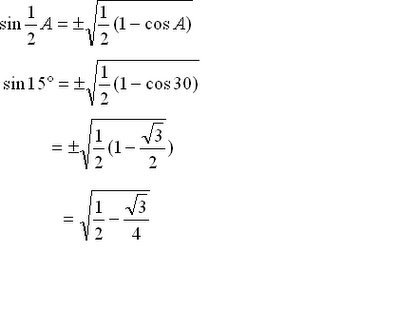




 this:
this:









