Chapter 2 Section 2

Chapter 2, Section 2
It is going to be very hard to top the posting by Nick, but I will try. I would like to present chapter 2, section 2: Measurement of Rotation. This section is very much about what the title says.
Key definitions/terms/ideas to note:

Periodic Functions: A function that repeats its values at regular functions
Coterminal Angles: Two angles in standard position are coterminal if and only if their degree measures differ by 360 degrees    
Example:



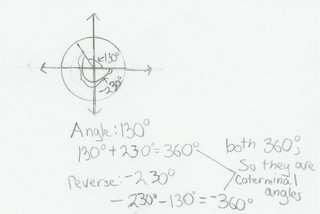
Reference Angle: The acute angle nearest to the x-axis
     Example:



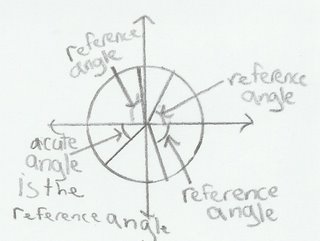
Basic Information:

1. Instead of using an x and y axis, use a u and v axis


2. When you have a positive angle measure, move counterclockwise. When you have a negative angle measure, move clockwise.

Examples:
     


Solving when given a large angle:

1. Divide the large angle, and divide it by 360 (representing a full revolution)


2. Multiply the decimal place of the answer by 360 (the whole numbers are the entire revolutions, and the decimal is the part of the revolution, so you multiply it by 360 to see what the actual degree measure is.

Example:
     Given: 4221 degrees      4221/360=11.725, 𝑡𝑎𝑘𝑒 .725 𝑎𝑛𝑑 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑦 𝑖𝑡 𝑏𝑦 360: 0.725360=261
       Therefore, there is a counter clockwise rotation of 261 degrees. The reference angle is 81 degrees.

Question: Find the reference angle when given a rotation of 4302 degrees.
     How to solve: divide 4302 by 360. Then from the 11.95 you get as a result, take the decimal and multiply it by 360. You should get a rotation of 342 degrees. From there, you know it is in the fourth quadrant, so take 360 minus 342, and you should get the reference angle.
The angle is 18 degrees.
__________________________________________________________
A reminder to katiecorr to post the next set of notes
__________________________________________________________
Here is a convenient website that calculates reference angle measures when you have a very large angle.

I figure people might as well know about one of Flintridge Prep’s most successful sports, so here is the Flintridge Prep Cross Country Wikipedia.

feel free to ask any questions
     

Section 1-6

As the first "student poster" to our Precalc Blog... I would like to present... Section 1-6! Section 1-6 is all about transformations and odd/even functions.

For our class notes and examples of what each type of graph looks like... visit: http://www.nickloui.com/precalc/1-6.htm

It's grouped into each type of transformation and should be fairly straightforward ( I tried to write neatly-ish ). Please email me if the website doesn't work (This is the first time I've tried to share my tablet notes), or better yet leave a comment!


Example Problem
The graph to the left is the graph of



Graph what the result of -f(x) would be.
Here's the Answer





Additional Internet Resources
Reflections of Graphs in y-Axis
Reflections of GRaphs in x-Axis
Both provide an interactive java applet to demonstrate the properties of f(-x) and -f(x)

A reminder to "navjit...he's more fly than sam?" to post the next set of notes!

Another note to help you out this year...
Our Precalculus Book is available online (the full text) which makes lugging it back and forth a bit easier. Click Here for the link of the textbook. Our Class Pass is: 1565-931fc25fe

For when you're bored -- there's an amazing parody of Shakespeare in Love that I learned about at film camp this year called George Lucas in Love and it's on one of my favorite websites Youtube! Click Here

Quiz 1.4-5 Quiz Topics

Here’s a list of topics for Wednesday’s quiz:

Precalculus Quiz 1.4-5 Topics
Domain and Range of functions
Calculate composite values from a graph
Plot composite values
Determine domain and range from a graph
Inverse functions – relationships of x and y
Sketching inverse functions given image of original function
Visual proof of functions and inverse functions
Determining domains of composite functions algebraically
Plotting inverse functions with calculator (function mode)
Plotting inverse functions with calculator (parametric mode)
Determining equations for composite functions algebraically
Plotting functions parametrically

I should be online tonight after 9pm for any last minute questions, and in my classroom tomorrow morning...

Good luck studying! If you need a break, check out these "criminals."

Blog Postings

As a reminder, the requirements for each blog posting will consist of:

• A review of the main point of the class lecture/demonstration.  This summary should highlight any relevant formulas and/or graphs and communicate your interpretation of the concept covered in class. (15 pts)  For this part of the posting, I am looking for quality, not quantity.


• An example problem, including a statement of the problem, the answer, and the solution method.  (For your first post, using an example covered in class is acceptable, for additional postings, original examples will be required.) (10 pts)


• A link to an additional Internet resource supporting the Topic of The Day. (5 pts)


• A reminder to the next BlogMaster of their responsibility to post. (5 pts)


• A “personalization” of your posting.  This personalization can be a comment about the day’s class, an image, a quotation, a question posed for discussion, a joke, or something else that reflects you as a student.  These personalizations must be in good taste!  (5 pts)

In addition to your posting, you will be expected to comment on a minimum of two (2) of your classmates postings during each quarter.  These comments must either further enhance your classmates’ understanding of the posted topic or further a discussion question posed in the original posting.

Additional Notes:

• Postings will be due within 24 hours of class.  I will post a schedule of class scribes for the first quarter once everyone has joined the class blog.


• For help with posting equations and graphs, please feel free to come ask me for assistance.


• Initially, the blogs will be hosted on blogger.com.  As the year progresses, we hope to migrate to an internal website.


• While we are on blogger.com, there is some software available through the website that allows creation/editing of posts via Microsoft Word.

Blog Policies

There are some things I want you to remember about blogging. Many of things have been discussed by other teachers and classes, so I will paraphrase them here and try to give them proper credit:

First of all, our class will not be the only people to view our postings. The Internet is accessible almost everywhere these days, and even if a post is deleted, there’s no guarantee that the posting hasn’t been copied and propagated to other sites or linked to from those sites. This has a couple of implications:

First, privacy. We will only be using first names on the site. If I post pictures or video, no one will be identified, other than “Mr. French’s class”. Do not use pictures of yourself for your profile here. If you want a graphic image associated with your profile, use an “avatar” – a picture of something that represents you but is not you. Here’s a link to a fun image creator.

Second, etiquette, appearance and common sense. Bud the Teacher has these suggestions, among others:

1. Students using blogs are expected to treat blogspaces as classroom spaces. Speech that is inappropriate for class is not appropriate for our blog. While we encourage you to engage in debate and conversation with other bloggers, we also expect that you will conduct yourself in a manner reflective of a representative of this school.


2. Never EVER EVER give out or record personal information on our blog. Our blog exists as a public space on the Internet. Don’t share anything that you don’t want the world to know. For your safety, be careful what you say, too. Don’t give out your phone number or home address. This is particularly important to remember if you have a personal online journal or blog elsewhere.


3. Again, your blog is a public space. And if you put it on the Internet, odds are really good that it will stay on the Internet. Always. That means ten years from now when you are looking for a job, it might be possible for an employer to discover some really hateful and immature things you said when you were younger and more prone to foolish things. Be sure that anything you write you are proud of. It can come back to haunt you if you don’t.


4. Never link to something you haven’t read. While it isn’t your job to police the Internet, when you link to something, you should make sure it is something that you really want to be associated with. If a link contains material that might be creepy or make some people uncomfortable, you should probably try a different source.

Are there other considerations we should take into account? Use the comment feature to add any others or to clarify/expand on one of the above.

Welcome

Congratulations! You found our class blog! You might want to bookmark this page or add it to your favorites. This is where we as a team will hopefully create a resource to help us conquer any issues that arise during our class this year. This is the place to talk about what’s happening in class; to ask a question you didn’t get to ask in class; to share your knowledge with fellow classmates and any other Internet users who choose to read our notes;…and most importantly it’s a place to reflect on what we’re learning.

A large part of retaining knowledge requires reviewing and discussing new information on a regular basis. This blog is intended to help each of you do just that. Between creating your own posts and commenting on your classmates’ posts, you will have the opportunity to explore each of the topics we cover this year in greater depth. I hope you will use this forum to help yourself and your classmates in whatever ways you can think of.

Blogging Prompt

Occasionally I will include a posting of my own, either to clarify a concept or to generate some further discussion. These postings will have a title similar to the one above this paragraph.

To get things rolling, here’s a question for you to think about and respond: Is God a mathematician? Why or why not?

Don’t forget to email me with the information I requested in class so I can include you on the team!