4.6 Inverse Trigonometric Relation Graphs

Graphs and Principal Branches of Inverse Trigonometric Functions:
In order to graph the inverse of sin, tan or cos you must switch the x and y variables. The inverse graphs are not functions. So, you have to choose a part of the graph in order for it to pass the vertical line test and be a function. You do this by restricting the domain of the graphs so that only the principal branch shows. Also, be sure to include the origin (or make it as centrally located as possible) and if possible, make it positive. The Principal Branch must show all possible values.
The inverse graphs can be graphed using the parametric mode. For example to graph arctan you would type: X1= tan(T) and Y1= T. This will give you the entire graph.
The function mode only graphs the principal branch of the inverse trigonometric function.

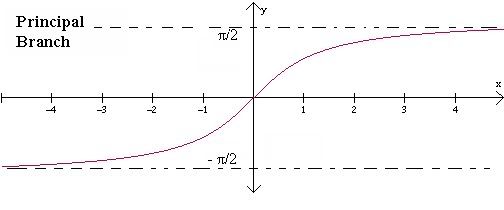
~The inverse graph of sine and its principal branch:

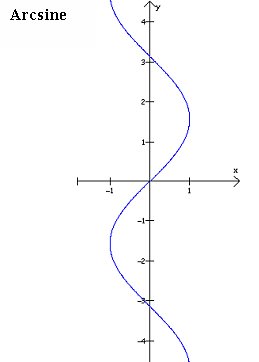
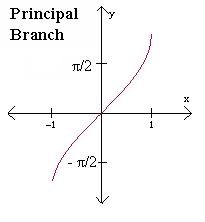
Domain: [-1,1]
Range:[-π/2, π/2]
Quadrants: I,IV

~The inverse graph of cosine and its principal branch: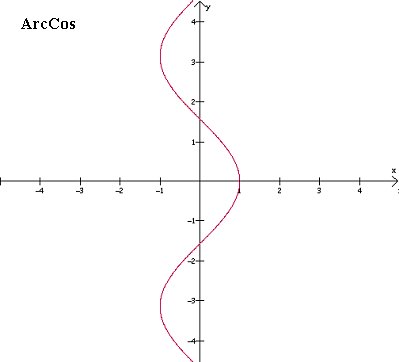

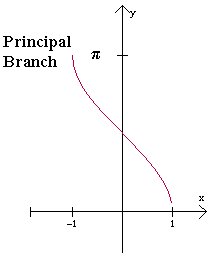
Domain:[-1,1]
Range:[0,π]
Quadrants: (I, II)

~The inverse graph of tan and its principal branch:

Domain: (∞, -∞) or all real numbers
range: (-Π/2, Π/2)
Quadrants: I, IV

~Also:

y=cot-1 x
Domain: (∞, -∞)
range: (0,Π)
Quadrants: I, II

y=sec-1 x
Domain: x ≥ 1
range: (0,Π) and y ≠ Π/2
Quadrants: I, II

y=csc-1 x
Domain: x ≥ 1
range: (- Π/2, Π/2) and y ≠ 0
Quadrants: I, IV

Exact Values of Inverse Circular Functions:

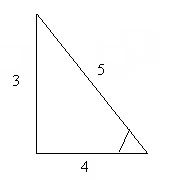
Create a triangle from the given information to geometrically solve the problem.

For example: cos (sin^-1(3/5))

From looking at the sin^-1(3/5) we know that the opp is 3 and the hyp is 5. Therefore the adj is 4 because of the pythagorean theorem.

Now that we have our triangle and angle set up we can find the cos of the angle which is the adj of hyp. The answer is 4/5.

The Composite of a Function and Its Inverse Function:

f(f^-1(x)) = x and f^-1(f(x)) = x

This is only true if x is in the range of the outside function and in the domain of the inside function.

Example Problem:

Problem:
tan^-1(tan(50º)) = ?

Method of Solution: Remember that f^-1(f(x)) = x if x is in the range of the outside function and in the domain of the inside function.
Answer: 50º is within the range of the outside function and the domain of the inside function, so the answer is 50º.

Link to an additional reference:

http://library.thinkquest.org/10030/2inverse.htm

This shows excellent inverse trigonometric graphs.

_________________________________________________________

JPD is just around the corner juniors!!! 5 days and counting. I would like you all to see the picture i have had to stare at all weekend while writing the descriptions for the silent auction items:
It's supposed to be Marilyn Monroe..

SAMMMM do not forget that you are next to post a blog!!

Good luck EVERYONE on your chapter 4 test on Wednesday (11/15)!!!

Hope my blog helps you when you are studying!!