Inverse Cosine Functions
Inverse Cosine Functions
Well, pretty much, this section is about finding the x-angle when a cosine relationship is given (in radians or in degrees). This can be done:
- Graphically
- Algebraically
Graphically
When the cosine relation is 1/2, both the positive and negative values of x plus every revolution of those two values suffice.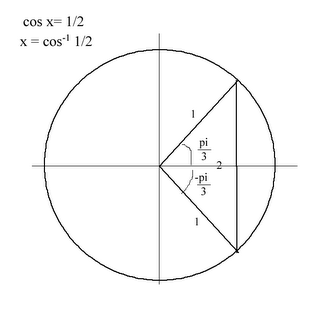
In this case, + or - π/3 + (2π)n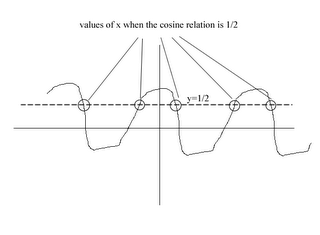
Algebraically
Before we begin, we must define a new term: Arccosine (or Arccos)
Arccos equals every arc or angle whose cosine is a given number.
Arccos = + or - anticos + (2π)n
These are the algebraic steps: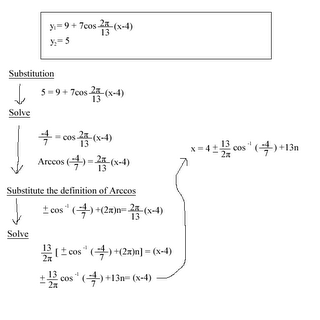
Finally, x = 8.508 + 13n or -.508 + 13n.
Yay!!! We're done!
Here's a link that talks about this section. Beware, it's pretty technical, but it's all I could find. http://mathworld.wolfram.com/InverseTrigonometricFunctions.html
Kaori... Guess what? You're our next scribe. Lucky You!!!!
Here's my personalization:
This guy is my hero. He is soooooooooo good at the ukelele. It's also really relaxing. http://www.youtube.com/watch?v=O9mEKMz2Pvo
posted by Anonymous @ 8:34 PM
3 comments
3 Comments:
For some reason, the letters are too small to see on the first half of the blog. What you can do is copy the text into Microsoft Word and enlarge them. Sorry for the inconvenience.
The letters weren't hard for me to read. The steps for solving the equations algebraically were easy to follow and they were helpful because I was a little confused on how to solve the equations. You could have included how to solve the equations numerically, but other than that, your blog is very good!
When we first learned about ARCCOS, it kind of intimidated me with the lengthy process and all, but this blog really breaks it down well... i suppose it's not so bad now. Also, your sinusoid graph is cute!
Post a Comment
<< Home