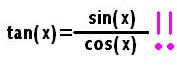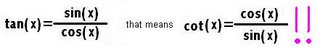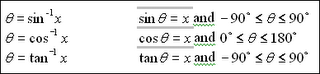Chapter 3 Test Topics

Here’s a list of topics for Thursday’s test:

Precalculus Chapter 3 Test Topics:
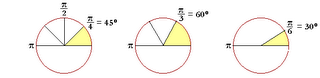
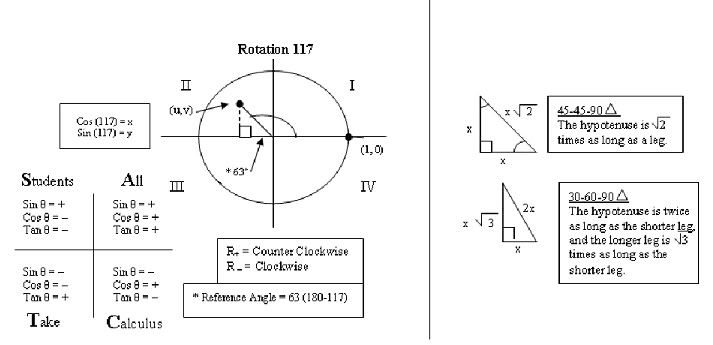
Radians to degrees (special angles)
Degrees to radians (special angles)
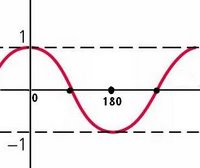
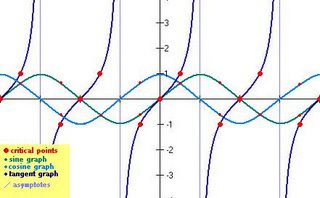
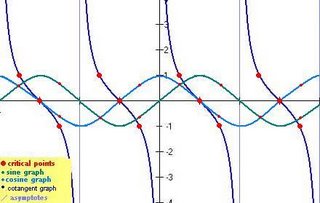
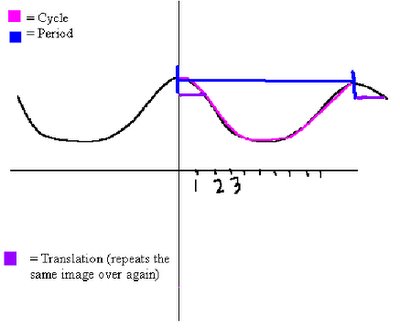
Sketch a sinusoidal graph given an equation
Demonstrate the concept of radians by wrapping an axis around a circle
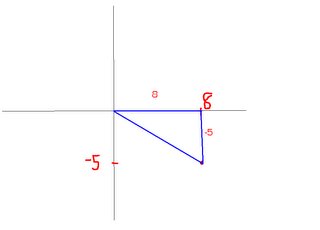
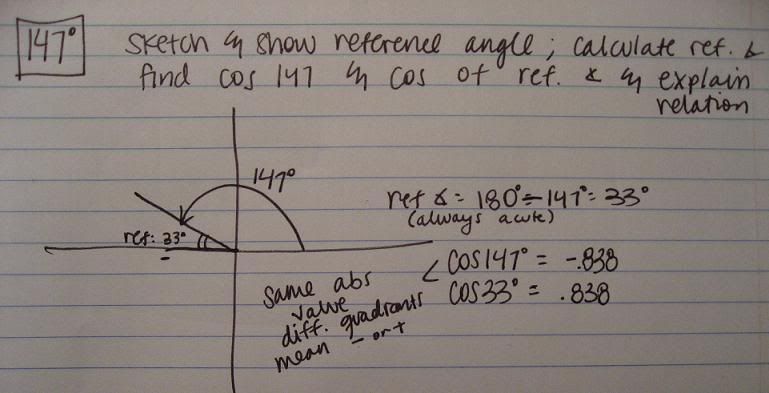
Sketch an angle in radians
Show the steps necessary to convert from radians to degrees, or vice versa
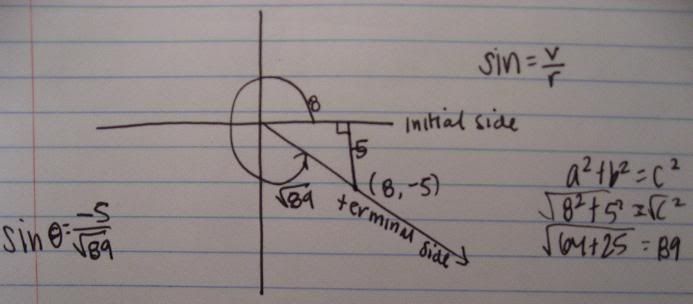
Position/Locate a radian angle
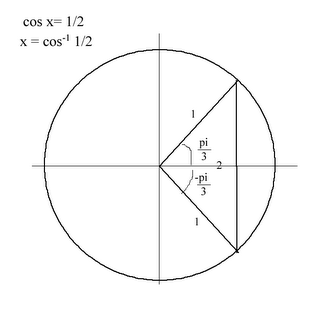
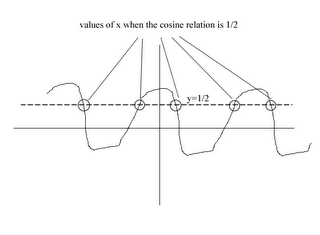
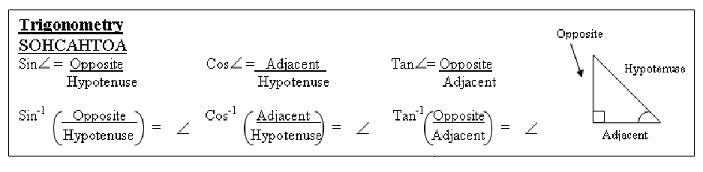
Inverse trigonometric functions
The meaning of arccosine
The definition of arccosine
A visual interpretation of radians and arclength
Determining a radian measure of an angle
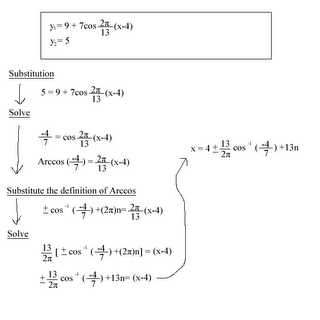
Determining a sinusoidal equation from a graph – sine and cosine
Word problem! Work with the given situation graphically, numerically and algebraically.

That’s it! The format is as expected – ½ calculator, ½ Non-Calculator. I’ll be in my classroom on Wednesday after school and before school on Thursday. I’ll also be available online later on Wednesday evening. If you have specific questions Wednesday night, email me!

See you in class!

"Sometimes when I get up in the morning, I feel very peculiar. I feel like I've just got to bite a cat! I feel like if I don't bite a cat before sundown, I'll go crazy! But then I just take a deep breath and forget about it. That's what is known as real maturity."
- Snoopy

3-7 Sinusoidal Functions as Mathematical Models

BOTTOM LINE: WORD PROBLEMS
AAAAAAAAHHHHHHHHHHHHHHH!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

BUT HAVE NO FEAR...cause it's actually not that bad

What you need to do is read the problem, and use the information given to find these four key facts::

• amplitude
• sinusoidal axis
• period
• phase displacement

also, keep in mind whether you want your equations to be in radians or degrees, and don't forget to set your calculator mode accordingly!

another note: when to use sin and when to use cos

• SIN:: if the information in the problem speaks about a midpoint
• COS:: if the information in the problem speaks about a high point

So, here are the steps in a more direct form:

1. look for the four keys and write an equation
2. decide whether you want radians or degrees (don't forget to set the calc mode!!)
3. use your equation to answer the questions in the problem

HAVE FUN GUYS!!!

**More importantly i hope EVERYONE went to homecoming and had a GRRRRRRREAT time!!


If you guys don't already know, there is a civil war going on in Uganda. One thing that the "rebels" are doing is creating armies of children. Why? Because there are so many of them and they don't care if they die. What they do is kidnap the children and train them to become killers, thiefs, and rapists, some as young as 5 years old. The children are threatened into joining because they kill the disobedient ones in front of their eyes. Many of these children want desperately to get out of this situation and sleep in the streets to try to hide at night. There's an organization called INVISIBLE CHILDREN which helps raise awareness and support for these children. They have been growing and making an impact all over. I think it'd be awesome if you guys could take 5 minutes to read up what they're about or watch one of their videos. It REALLY touched me and I want to do everything I can for these kids.

www.invisiblechildren.com

SUPPORT A CAUSE!!!!

REMINDER TO GINA!!!

You're up next for the blog

Inverse Cosine Functions

Inverse Cosine Functions

Well, pretty much, this section is about finding the x-angle when a cosine relationship is given (in radians or in degrees). This can be done:

• Graphically
• Algebraically

Graphically

When the cosine relation is 1/2, both the positive and negative values of x plus every revolution of those two values suffice.

In this case, + or - π/3 + (2π)n

Algebraically

Before we begin, we must define a new term: Arccosine (or Arccos)

Arccos equals every arc or angle whose cosine is a given number.

Arccos = + or - anticos + (2π)n

These are the algebraic steps:

Finally, x = 8.508 + 13n or -.508 + 13n.

Yay!!! We're done!

Here's a link that talks about this section. Beware, it's pretty technical, but it's all I could find. http://mathworld.wolfram.com/InverseTrigonometricFunctions.html

Kaori... Guess what? You're our next scribe. Lucky You!!!!

Here's my personalization:

This guy is my hero. He is soooooooooo good at the ukelele. It's also really relaxing. http://www.youtube.com/watch?v=O9mEKMz2Pvo

Wednesday's Quiz Topics

Here’s a list of topics for Wednesday’s quiz:

Precalculus Quiz 3.3-5 Topics
Radians
Convert Radians to Degrees
Convert Degrees to Radians
Sinusoids (radians)
Sketch a sinusoidal graph from an equation
Determine a sinusoidal equation from a graph
Graphs of tangent, cotangent, secant and cosecant
Identify transformations of a sinusoid
Identify characteristics of a sinusoid
Analyze a sinusoidal situation given specific information (yes, the ever-present word problem!)

That’s it. I’ll be in early on Wednesday…

"Optimists are right. So are pessimists. It's up to you to choose which you will be."
- Harvey Mackay

Section 3.5 in the house!

Lession 3.5 by Paul Weitekamp

Ok guys, this section is about circular functions. It is basically the same kind of periodic functions we've dealt with before, but with radians instead of degrees.

So basically...
there are three key points to this section.

1. We have to distinguish between functions in degrees and functions with radians...

-Theta (the symbol won't show up) is used for functions with degrees.
-X is used for functions with radians.


2. The period for radians is found differently...

Whereas before in the equation: y=C+A sin B (x-D), B = 360/ period
With radians: B= 2Π/ period

3. Another important point we went over in class was that if you draw a line from the origin to the circumfrence of any unit circle, see figure below, then Cos x = u and Sin x = v.

This is true because the line from the origin to (u,v) is really just a radius to the circle and the radius = 1 in a unit circle. So....

Since Cos x = u/1 then, Cos x = u and Since Sin x = v/1 then, Sin x = v

Example Problem- What is the period of a sinusoid with the equation:

y= 6 + 3 sin ((Π/4) x- 7)

Ok then that's pretty much the lesson. Any questions don't be afraid to post them. And before i'm done i'd like to give a shout out to the homies in Virginia, keep it real.

LEO IS NEXT!?!?!??!?!

For more information see http://www.cis.edu.hk/sec/math/ib/higher/trig/CircFunc&Trig.htm

3-4 Radian Measures

So far, we have learned about degree measures on a unit circle. Now, we get to learn about radian measures!

Here's the basic info:

The concept of a radian:
π=circumfrance/diameter
In half of a circle, there are π number of radians.

Each of the curved lines represent one raidan in the unit circle.

In terms of a circle, a radian can be seen as the ratio of the length of the arc subtended by two radii to the radius of the circle.

Half of the circumfrance is π, so at 180°, the radian measure at 180 is π.

Converting radians to degrees and degrees to radians:

To convert degrees to radians, you multipy the angle measure in degrees and multiply it by π/180.

For example:

36°= 36 * π/180= 36π/180=π/5

and

To convert radians to degrees, you multiply the radian measure and multiply it by 180/π.

For example:

π/6 Radians:

π/6 * 180/π=180/6=30°

Special Angles:

Here are the special angles we get to learn about.

0° = 0 radians

30°=π/6 radians

45°= π/4 radians

60°=π/3 radians

90°=π/2 radians

180°=π radians

Other helpful stuff:

You can switch between degrees and raidans on your calculator by going to mode, and then choosing between radians and degrees.

In the angle menu:

You can give radians and it will give you degrees in radian mode if you choose the degree symbol.

You can also give degrees and get radians in the degree mode if you choose the rad option.

That's pretty much it!

Here's a good site to look if you need more info:http://www.themathpage.com/aTrig/radian-measure.htm

A Reminder to P Dubs....a.k.a. Paul to do the next posting!

Now for my personalization (which must be done in green)!

First, I have to say, the Prep Varsity Tennis Team beat Poly again today! Woo hoo! This is very exciting news and I expect many congrats from you all tomorrow...jk.

Also...here is a link for a really yummy recipe because cooking is fun and you should all do it too! They are spooky spice cookies just in time for Halloween!http://www.foodnetwork.com/food/recipes/recipe/0,,FOOD_9936_34566,00.html

Thursday's Quiz

Here’s a list of topics for Thursday’s quiz:

Precalculus Quiz 3.1-3 Topics
Sinusoids:
Cycles
Periods
Phase displacement
Critical points
Points of inflection
Concavity
Sketch a sinusoidal graph from an equation
Determine a sinusoidal equation from a graph
Graphs of tangent, cotangent, secant and cosecant
Identify transformations of a sinusoid
Identify characteristics of a sinusoid
Analyze a sinusoidal situation given specific information (yes, the ever-present word problem!)

That’s it. I’ll be in early on Thursday…

"There is nothing noble in being superior to someone else. The true nobility is in being superior to your previous self."
-Hindu Proverb

3.3 Graphs of Tangent, Cotangent, Secant, & Cosecant Functions

So basically, we're familiar with what the graphs of the sine and cosine functions look like.
We've got sine:

And we've got cosine:

OOh la la!
What 3.3 is all about is figuring out what the other trig functions' graphs will look like based on what we already know. Before we get to an example, let's go through some logical steps to find out what some of these functions should look like without using graphing calculators.

Let's start with a tangent graph; we should first find its relationship to the sine and cosine, since we've got those down!

therefore,

So when we graph the tangent, based this relationship we're going to have some critical points and noteable features. DUN DUN DUNNNNN!

• Whenever sin(x)=0, these will be the x-intercepts, since that would mean tan(x)=0 as well.
• Whenever sine and cosine are equal, tangent=1, and whenever sine and cosine are opposites, tangent= -1.
• Asymptotes occur where cos(x)=0, since that would mean tan(x)=undefined *this means that there is an asymptote every 1/2 period or every 180 degrees*

Let's graph!

Next...let's see if we can graph the cotangent. Same process

1. Find the relationship...since

and that means we can make some...

2. Important inferences:

• Whenever cos(x)=0, these will be the x-intercepts, since that would mean cot(x)=0 also
• Whenever sine and cosine are equal, cotangent=1, and whenever sine and cosine are opposite, cotangent= -1;
• Asymptotes occur where sin(x)=0, since that would mean cot(x)=undefined; this means that there is an asymptote every 1/2 period, or every 180 degrees, just like the tangent!

3.Graph:

NOW! As an example, see if you can graph the secant and cosecant functions on your own using what you already know! Then check out how you did by referring back to the post.

Solutions:

Secant:

1. Find the relationship:

2.Critical points/noteable notes:

• When cos(x)=1, sec(x)=1 and when cos(x)= -1, sec(x)= -1
• Since secant and cosine are reciprocals, as the cosine gets bigger, the secant gets smaller, and as the cosine gets smaller, the secant gets bigger
• Asymptotes will occur whenever cos(x)=0, because at those points, sec(x) = undefined; this means that a period occurs every 360 degrees (this is where the pattern begins to repeat all over again)

3.Graph:

Cosecant:

1. Find the relationship:

2. Critical points/noteable notes:

• When sin(x)=1, csc(x)=1 and when sin(x)= -1, csc(x)= -1
• Since cosecant and sine are reciprocals, as the sine gets bigger, the cosecant get smaller, and as the sine gets smaller, the cosecant gets bigger
• Asymptotes occur whenever sin(x)=0, since that would mean csc(x)=undefined

3. Graph:

*note that cosine and secant are even functions and that tangent and cotangent functions are odd.

EXTRA sources: If you believe in SparkNotes, or if you don't, here are some other places that you can find these same graphs. Personally, I believe my post is better, but in any case...

*****Christina, you're next!*****

Finally, for all you musicians out there, here are some great (evil) jokes specified for instruments/vocalists/conductors, etc. Just to let you guys know as a sidenote, NONE of the oboe ones are true!!!

Thursday's Test Topics

Here’s a list of topics for Thursday’s test:

Precalculus Chapter 2 Test Topics:
Sketch an angle given a point on the terminal side or a measurement in degrees.
Determine the reference angle’s location and measure.
Determine the six trigonometric functions for the angle.
Describe transformations to a trigonometric graph and determine the resulting function.
Determine trig functions based on right triangles.
Determine the principal branch of a trigonometric function.
Describe the characteristics of a principal function (one-to-one).
Discuss the reason for a principal branch.
Sketch a graph of a function given a description.
Determine type of function based on graph.
Find trigonometric functions with your calculator.
Determine reference angles and discuss their relationship to primary angles.
Triangle word problems – determine angles and sides.

That’s it! The format is as expected – ½ calculator, ½ Non-Calculator. I’ll be in my classroom until 3 on Wednesday and before school on Thursday. I’ll also be available online after Back to School Night on Wednesday.

See you in class!

Lesson 3.1, 3.2 - Sinusoids

Yay...My First Blog Post! ^_^

Lessons
3.1 - Sinusoids: Amplitude, Period, and Cycles
3.2 - General Sinusoidal Graphs

Equation:
y=C+A sin B(x - D)
or
y=C+A cos B(x- D)

Amplitude (A) - How far we go to reach the Minimum or the Maximum from the sinusoidal axis.

Vertical Translation (C) - Location of the sinusoid. (Essentially the location of the sinusoidal axis.)

Phase Displacement (D) - How far we shift to the right or left. (Basically the x-translation)

To find the period of the graph we go like this

Period = 360/ |B|
360/absolute value of B
Note that this is also a lot like the X-dilation in the previous lessons.












Example Problem -

Find the Amplitude, the phase displacement, the sinusoidal axis and the period of this function.

y=8-3 sin (1/4)(x+30)




Solution -
Amplitude = 3
Phase Displacement = -30
Sinusoidal Axis - y=8
Period = 4*360 = 1140

Additional Internet Resources:

A webpage that explains a lot of things about sinusoids

_______________________________________________

Reminder! The next blog poster is...Amira! Have fun!

_______________________________________________

Hmmm...now for my personalization...
it may not be as appealing to some of you as to me...but
Yes, I want you all to go to the varsity homecoming game! Yes, it really is that important to me so please come!!! It is on the October 28 at like 7. You'll know the details soon enough, we'll really enjoy your support.
Oh yeah, just a reminder for all of you, we are required to post 2 comments for the blogs during each quarter so just so you know!

2-5: Inverse Trigonometric Functions and Triangle Problems

Hey guys... =]

Definitons:

If x is the value of a trigonometric function at angle θ, then the inverse trigonometric functions are:
The principal branch is the portion of the graph that is one-to-one (invertible). When finding the value of an angle from an inverse trigonometric function, your calculator gives you the value that rests on this branch of the graph. This is to ensure the graph of the inverses of the sin/cos/tan functions will also be functions.

For example:

The domain and range of sin x is the range and domain of its inverse.

Example triangle problem:
A ship is passing throught a strait and is 2400 m away from an island as determined by radar. Later, the radar determines that the ship is 2650 m away. By what angle (theta) did the ship's bearing change?

Explanation: Cosine is a ratio of adjacent over hypotenuse, in this case 2400/2650. The inverse cos function is looking for the angle whose ratio of adj/hyp is 2400/2650. We solve to get 25.1 degrees.

Be Careful!:

Additional Internet Resources:
Inverse trig functions
Useful symbols (such as theta)

Edward - Remember to post the next set of notes!

If you have some time, I thought this was pretty amusing.
Make a "Text-Image"
Click "Convert" to make your own.

2.4 notes...ya its kinda like that sierra mist

Hey peeps...

Section 2.4 Notes!!!

Values of the Six Trigonometric Functions

The six trig funcions are :

1. Sine = Opposite/Hypotenuse
2. Cosine = Adjacent/Hypotenuse
3. Tangent = Oppoiste/Adjacent
4. Cosecant = Hypotenuse/Opposite
5. Secant = Hypotenuse/Adjacent
6. Cotangent = Adjacent/Opposite

**Note**

I tend to look at these functions in pairs. Sine and Cosecant are reflections of each other, Cosine and Secant are reciprocals of each other, and Tangent and Cotangent are reflections of each other.

**End Note**

All of the Trig functions for 180 degrees:

1. Sin = 0
2. Cos = -1
3. Tan = 0
4. Csc = undefined
5. Sec = -1
6. Cot = undefined

Find all the trigometric functions for theta in the triangle picture below

1. Sin = 5/10
2. Cos = 8/10
3. Tan = 5/8
4. Csc = 10/5
5. Sec = 10/8
6. Cot = 8/5

Find the trigmatic functions of the point (8,-5)

1. Sin = -5/(rad 89)
2. Cos = 8/(rad 89)
3. Tan = -5/8
4. Csc = (rad 89)/-5
5. Sec = (rad 89)/8
6. Cot = 8/-5

**Note**

I am really srry it says "rad 89" instead of having a radical sign. Copy and paste doesn't work and I don't use word I use word perfect so the add on wont work. If anyone could tell me how I could put in the actual symobol for rad I would greatly appreciate it. Thnanks!!!

**End Note**

EXAMPLE PROBLEM

Find all six trigmatic functions for the angle inbetween the sides with lengths 10 and 20

Answers with work!!!

1. Sin (opposite/hypotenuse) = 15/20 =3/4
2. Cos (adjacent/hypotenuse) = 10/20 = 1/2
3. Tan (opposite/adjacent) = 15/10 = 3/2
4. Csc ( hypotenuse/opposite) = 20/15 = 4/3
5. Sec (hypotenuse/adjacent) = 20/10 = 2
6. Cot (adjacent/opposite) = 10/15 = 2/3

Additional links

history of trig functions!

REMINDER TOO MADI!!! CUZ UR THE LUCKY PERSON WHO GETS TO FOLLOW ME!!!!

Ok now its my personalization...I have thought really long and hard about this and I've decided there is only one thing to go with a chuck norris joke...cuz hes just that kool.

"Chuck Norris appeared in the "Street Fighter II" video game, but was removed by Beta Testers because every button caused him to do a roundhouse kick. When asked bout this "glitch," Norris replied, "That's no glitch.""

Thursday's Chapter 1 Test Topics

First, I've decided to postpone the Chapter 2 Application problem until next Friday (October 13th). Remember, your problems should reflect reality - if you need to restrict the domain of the problem, or somehow manipulate your scenario, by all means do so!

Ok, here are the topics:
Precalculus Chapter 1 Test Topics:
· Determine domain and range of a function from a graph
· Given a graph, sketch a given transformation
· Determine if an inverse relation is a function and justify
· Plot a function and its inverse relation using parametric mode
· “Shopping Cart”-type problem
· Determine the domain of a composite function consisting of restricted original functions
· Plot a composite function with a restricted domain
· Determine values of a composite function or explain why no value can be obtained
· Even and Odd functions
· Identify types of functions from equations and/or graphs
· Determine the inverse of a function and plot it on the same set of axes with the original function
· Explain the visual relationship on a graph between a function and its inverse

Mathematician or not?

2.3 Sine and Cosine Functions

2.3 Sine and Cosine Functions

Periodic Function: Function f is a periodic function of x if and only if there’s a number P for which f(x-p)=f(x). If P is the smallest such number then P is the period of f.
Sine and Cosine are both periodic functions.

Here is a valid website if you need more help on this subject!

Sam!! Do not forget that you are the next person to post! So, take PERFECT notes on Monday, Oct. 2nd

EVERYONE should come to the Prep vs. Webb varsity volleyball game on Tuesday at 4:30p. Also, we play Rio Hondo on Thursday (same time)! We need all the support we can get! This week will be an important one for us! Good luck in your own sports everyone! Hope your weekend went well!! Don't forget to start planning your Halloween costumes!! Yes, it's finally October!!