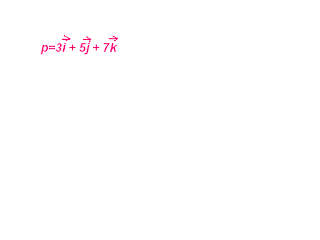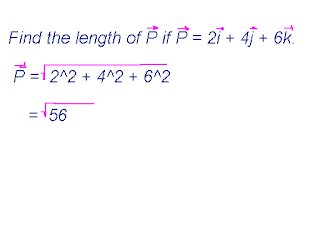10 - 8 : Vector Equations of Lines in Space
10-8 : Vector Equations of Lines in Space
First of all let me explain the purpose of this lesson. It is very simple. If you have a line, and random line through space, and one point on that line, and a unit vector, you can find the equation of the position vectors to any point on that line. You must choose a distance, or "d" to work with. "d" is just a distance or magnitude, which represents the distance to the next point on the line you want to find.
Ok so i find that it is easier to explain this verbally rather than graphically, however I know some people would like to know precisely where everything im talking about is in a diagram so, I decided to make a diagram which u can refer to whenever your heart so desires!

ok, i am not a very good "graph maker," so I color coded it so that I can try to make up for that with my explanation.
- the red A is referred to as P0 in the book, and is the given point on the line.
- the pink vector is referred to as vector P0, and is the vector to the given point.
- the blue line is the line, and the unit vector that is used, is the unit vecotr of this line.
- the yellow portion of the line is "d" or the distance from point A to point B.
- the red B is the point which the position vector we are finding the equation for.
- the orange vector is the actual position vector we are finding the equation of.
In essence, we are just adding vectors. Or in the case of the diagram, we are adding the pink vector to the yellow vector, in order to get the orange vector. Mathematically we would say, we are adding vector Po and vector PoP.
*note : Vector du = Vector PoP*
The method we use to figure out the equation of the position vector is :
- Vector v = vector Po + d(unit vector)
This is when we are given the unit vector.
- Vector v = (xo + c1*d) + (yo + c2*d) + (zo + c3*d)
This is when we must work with the cosines instead of being given the equation.
Sample problem when given the unit vector.
Problem : The point is (5,11,13) and the unit vector is 3/7 i + 6/7 j + 2/7 k. D = 5. Find vector PoP (v).
Work :
Vector v = (5 i +11 j +13 k) + 5(3/7 i + 6/7 j + 2/7 k)
Vector v = (5 i +11 j +13 k) + (15/7 i + 30/7 j + 10/7 k)
Vector v = 7.143 i + 15.286 j + 14.429 k
Answer : Vector v = 10.714 i + 47.143 j + 18.57 k
Now I will show you a problem where we are given the cosines
Problem : The point is (5,3,-1) and the cosines are : c1 = 6/11, c2 = -2/11, and c3 = 9/11. D=5.
Work :
vector v = (5 + (6/11)(5)) i + (3 + (-2/11)(5)) j + (-1 + (9/11)(5)) k
vector v = (5 + (30/11)) i + (3 + (-10/11)) j + (-1 + 45/11) k
vector v = 7.727 i + 2.091 j + 3.091 k
Answer : vector v = 7.727 i + 2.091 j + 3.091 k
Both of these methods are purely plug and chug. They are a sinch and aren't ridiculously long either. All in all they are pretty darn awesome.
Challenge Problem!!!
Problem : Timmy is looking at the great wall of china. He knows that the exact point he is staring at is located at (5,10,20). He knows that the unit vector for the wall is
(9/17) i + (12/17) j + (8/17) k. He wants to know the position vector from him to the point 10 feet to the right of the one he is looking at currently. Help Timmy find the position vector.
Work :
first set up the problem
vector v = (5 i +10 j +20 k) + 10 ((9/17) i + (12/17) j + (8/17) k)
distribute the distance
vector v = (5 i +10 j +20 k) + (90/17) i + (120/17) j + (80/17) k
group according to like terms
vector v = (5 i + (90/17) i) + (10 j + (120/17) j) + (20 + (80/17) k)
add like terms
vector v = 10.294 i + 17.059 j + 24.706
Answer : vector v = 10.294 i + 17.059 j + 24.706
This concludes MY lesson. But if you really want to indulge yourself in a very vector-like bliss, i suggest you check out http://mathforum.org/~klotz/Vectors/vectors.html.
This site literally has everything on vectors. It has formulas, but also explains them. It also has pretty good pictures and diagrams to go with them. So everyone, even Alvin and the chipmunks, should go check this out!
Here is a little bit of me : This is the cover the the Silversun Pickups debut cd, Carnavas. It is absolutely phenominal in every way. So I insist you go buy it now, or have me burn you a copy, because they are just that kool. They kill 2 stones with one bird, just like chuck norris.

REMINDER TO PAUL!!!! YOU ARE NEXT!!!!!!!!!!



























 Thanks to our handy dandy calculators, we can easily find all of the values in the binomial distribution, hooray!
Thanks to our handy dandy calculators, we can easily find all of the values in the binomial distribution, hooray!