9.3 Two Counting Principles

9.3 Two Counting Principles

Independent Event:

The way one event occurs does not affect the way the other could occur.

Mutually Exclusive events:

The occurrence of one event excludes the possibility the other will occur.

n(A or B) = n(A) + n(B)

(the number of A or B is the number of A + the number of B)

Properties: Two Counting Principles:

Let A and B be two events that occur in sequence.

Then n(A and B) = n(A) * n(B)

Where n(BA) is the number of ways B can occur after A has occurred.

When A and B are independent = n(A) * n(B)

Overlapping Events:

n(A or B) = n(A)+ n(B) -n(A 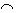B)

(number of ways A can occur + number of ways B can occur – number of ways A and B overlap)

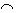· means “and” on the intersection of A and B

· No common area means that A and B are mutually exclusive and “-n(A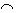 B)”

equals zero

Example Problem:

A salad menu consists of 4 toppings and 5 dressings. Find the number of different ways you could select..

a. a topping or a dressing

b. a topping and dressing

Work:

a. Mutually Exclusive events: n(A or B) = n(A) + n(B); n(dressing or topping) = n(4) + n(5) = 9

b. Two Counting Principles where they are both independent: n(A and B) = n(A) * n(B); n(dressing and topping) = n(dressing) * n(topping) = 20

Answer

a. 9

b. 20

Extra Help:

http://www.gomath.com/htdocs/lesson/probability_lesson1.htm

Reminder to NICK LOUI!!! You are up next!!!

I am about to go to a prom meeting so here is a fun little fact (sorry sophomores): PROM IS IN 54 DAYS!! Start thinking about dresses, dates, and plans!!!