Section 7.2: Identifying Functions from graphical patterns

7-2: Identifying Functions From Graphical Patterns
This section is basically a review. It covers the four basic functions (linear, quadratic, power, and exponential) and demonstrates how to find an equation when given a set of coordinates and a function. The functions, with their names and equations, are shown below.
Linear Function
general equation: y=ax+b
parent: y=x
transformed: y-y1=a(x-x1)
Quadratic Function
general: y=ax^2+bx+c (a is not equal to 0 and b and c are contants)
parent: y=x^2
transformed: y-k=a(x-h)^2 (k and h are the coordinates of the vertex)
a>0


a<0 style="color: rgb(0, 0, 0);">When a is positive, the parabola is facing up, like a smile :) and when a is negative, the parabola faces down, like a frown :(
b>1

 0<b<1
0<b<1 b<0
b<0
Power Function
general: y=ax^b (a and b are not equal to 0)
parent: y=x^b
transformed: y=a(x-c)^b+d
Eponential Function
general: y=ab^x
parent: y=b^x
transformed: y=ab^(x-c)+d
b>1
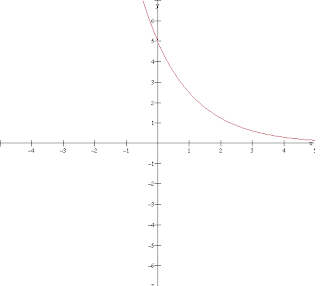
0<b<1

The equation for a logarithmic function with base 10 is y=10^x
The equation for a natural logarithmic function with base e is y=e^x
Here is an example problem:
What is the equation of a power function with the coordinates (6, 151.2) and (4, 44.8)?
The FIRST thing to do is to remember the equation for a power function, which is y=ax^b
then plug the coordinates into the equation. 44.8=a(4)^b and 151.2=a(6)^b. With power functions, you divide the equations to find a and b.
151.2/44.8=a(6)^b/a(4)^b
When you divide the equations, the a cancels out and you can then find the b exponent
you get...
3.375=6^b/4^b= (6/4)^b
3.375=1.5^b
To find the b exponent, take the log of both sides.
log(3.375)=log(1.5)b <---- the b is no longer an exponent b=log(3.375)/log(1.5)
b=3
Now plug b into one of the equations from before.
44.8=a(4)^3
a=44.8/64
a=.7
then you plug a and b into the general power function equation.
y=.7x^3 <--- answer!!
** When finding equations for exponential and power functions, you use this method and divide the equations to find the values of a and b. For quadratic functions, you can use matrices. For linear functions, you simply plug the coordinates into the equation.
Extra help!!!!!
www.vhcc.edu/pc1spring99/basic_function_families/introduction_to_function_families.htm#The%20four%20basic%20functions%20and%20Otheir%20families
There's a new schedule, so good luck to whoever goes next!
general equation: y=ax+b
parent: y=x
transformed: y-y1=a(x-x1)
Quadratic Function
general: y=ax^2+bx+c (a is not equal to 0 and b and c are contants)
parent: y=x^2
transformed: y-k=a(x-h)^2 (k and h are the coordinates of the vertex)
a>0


a<0 style="color: rgb(0, 0, 0);">When a is positive, the parabola is facing up, like a smile :) and when a is negative, the parabola faces down, like a frown :(
b>1

 0<b<1
0<b<1 b<0
b<0Power Function
general: y=ax^b (a and b are not equal to 0)
parent: y=x^b
transformed: y=a(x-c)^b+d
Eponential Function
general: y=ab^x
parent: y=b^x
transformed: y=ab^(x-c)+d
b>1
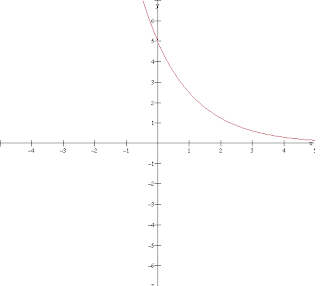
0<b<1

The equation for a logarithmic function with base 10 is y=10^x
The equation for a natural logarithmic function with base e is y=e^x
Here is an example problem:
What is the equation of a power function with the coordinates (6, 151.2) and (4, 44.8)?
The FIRST thing to do is to remember the equation for a power function, which is y=ax^b
then plug the coordinates into the equation. 44.8=a(4)^b and 151.2=a(6)^b. With power functions, you divide the equations to find a and b.
151.2/44.8=a(6)^b/a(4)^b
When you divide the equations, the a cancels out and you can then find the b exponent
you get...
3.375=6^b/4^b= (6/4)^b
3.375=1.5^b
To find the b exponent, take the log of both sides.
log(3.375)=log(1.5)b <---- the b is no longer an exponent b=log(3.375)/log(1.5)
b=3
Now plug b into one of the equations from before.
44.8=a(4)^3
a=44.8/64
a=.7
then you plug a and b into the general power function equation.
y=.7x^3 <--- answer!!
** When finding equations for exponential and power functions, you use this method and divide the equations to find the values of a and b. For quadratic functions, you can use matrices. For linear functions, you simply plug the coordinates into the equation.
Extra help!!!!!
www.vhcc.edu/pc1spring99/basic_function_families/introduction_to_function_families.htm#The%20four%20basic%20functions%20and%20Otheir%20families
There's a new schedule, so good luck to whoever goes next!
Labels: 7.2

0 Comments:
Post a Comment
<< Home