3.3 Graphs of Tangent, Cotangent, Secant, & Cosecant Functions

So basically, we're familiar with what the graphs of the sine and cosine functions look like.
We've got sine:

And we've got cosine:

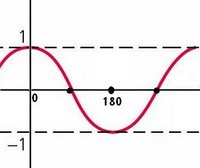
OOh la la!
What 3.3 is all about is figuring out what the other trig functions' graphs will look like based on what we already know. Before we get to an example, let's go through some logical steps to find out what some of these functions should look like without using graphing calculators.

Let's start with a tangent graph; we should first find its relationship to the sine and cosine, since we've got those down!

therefore,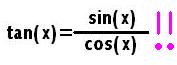

So when we graph the tangent, based this relationship we're going to have some critical points and noteable features. DUN DUN DUNNNNN!

• Whenever sin(x)=0, these will be the x-intercepts, since that would mean tan(x)=0 as well.
• Whenever sine and cosine are equal, tangent=1, and whenever sine and cosine are opposites, tangent= -1.
• Asymptotes occur where cos(x)=0, since that would mean tan(x)=undefined *this means that there is an asymptote every 1/2 period or every 180 degrees*

Let's graph!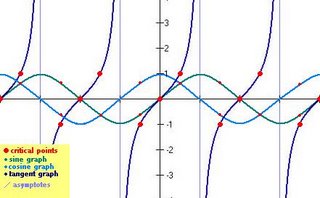

Next...let's see if we can graph the cotangent. Same process

1. Find the relationship...since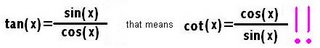

and that means we can make some...

2. Important inferences:

• Whenever cos(x)=0, these will be the x-intercepts, since that would mean cot(x)=0 also
• Whenever sine and cosine are equal, cotangent=1, and whenever sine and cosine are opposite, cotangent= -1;
• Asymptotes occur where sin(x)=0, since that would mean cot(x)=undefined; this means that there is an asymptote every 1/2 period, or every 180 degrees, just like the tangent!

3.Graph: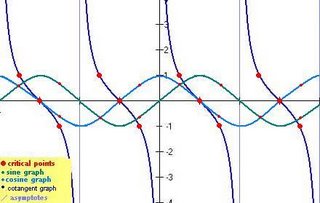

NOW! As an example, see if you can graph the secant and cosecant functions on your own using what you already know! Then check out how you did by referring back to the post.

Solutions:

Secant:

1. Find the relationship:

2.Critical points/noteable notes:

• When cos(x)=1, sec(x)=1 and when cos(x)= -1, sec(x)= -1
• Since secant and cosine are reciprocals, as the cosine gets bigger, the secant gets smaller, and as the cosine gets smaller, the secant gets bigger
• Asymptotes will occur whenever cos(x)=0, because at those points, sec(x) = undefined; this means that a period occurs every 360 degrees (this is where the pattern begins to repeat all over again)

3.Graph:

Cosecant:

1. Find the relationship:

2. Critical points/noteable notes:

• When sin(x)=1, csc(x)=1 and when sin(x)= -1, csc(x)= -1
• Since cosecant and sine are reciprocals, as the sine gets bigger, the cosecant get smaller, and as the sine gets smaller, the cosecant gets bigger
• Asymptotes occur whenever sin(x)=0, since that would mean csc(x)=undefined

3. Graph: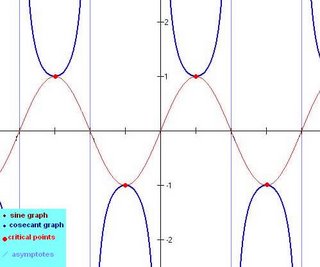

*note that cosine and secant are even functions and that tangent and cotangent functions are odd.

EXTRA sources: If you believe in SparkNotes, or if you don't, here are some other places that you can find these same graphs. Personally, I believe my post is better, but in any case...

*****Christina, you're next!*****

Finally, for all you musicians out there, here are some great (evil) jokes specified for instruments/vocalists/conductors, etc. Just to let you guys know as a sidenote, NONE of the oboe ones are true!!!